昨天我們談到機器學習基本上就是一個相當複雜的函數，我們蒐集了許多的資料，試圖讓這個函數能夠擬合問題的函數。

當我們要使用機器學習解決這個問題時，大致上會經歷幾個步驟

1. 定義函數
   定義出模型的架構，如：
2. 將資料輸入進模型，並評估模型好壞
   透過評估模型的好壞，接下來就能夠知道怎樣調整會比較好。
3. 調整參數大小
   依據評估調整參數。

正式前往下一步之前我們必須要提兩個問題。

1. 這個"相當複雜的函數"如何描述
2. 要如何讓函數擬合問題

對於第二個問題，機器學習上的做法會是製作出一個評估模型好壞的 損失函數(Loss Function) ，接下來透過這個函數給我的評估結果，調整模型的函數參數。
因此在這一篇我們先來談談 如何表達一個模型 以及 如何評估一個模型好壞。

模型表示

昨天我們舉了一個預測房價的例子。在這個例子當中我們用一個極其簡單的函數 來描述它，所以它看起來是一條直線，而透過一些方法我們得知在這裡最佳的 是 和 。

設定了 這件事實際上就是在描述一個模型。
當然，也可以設定更加複雜的模型，例如 或是 。

現在的狀況下輸入都只有一個特徵，也就是 房子大小，所以可以單純用一個純量(scalar)來表示 。不過當特徵開始變多，像是透過 房子大小 以及 房間數量 來評估價格時，也許假設成底下這個樣子。

也就是說，除了原先的 房子大小() 以外，還需要考慮 房間數量() 了。
若是維持最高項為二次方，那今天再新增一個特徵如 到市中心的距離()，那麼也許就會變成

當要考慮的特徵越來越多時，單純的加法與乘法描述似乎會過於冗長，因此更多時候我們會使用的是矩陣與向量來表示一個模型。以上面兩個特徵來說，矩陣表達會變成

更多時候我們會把前面的係數像是 和 都變成一個矩陣如 來表示。
後面的 和 則用 來表示。
最後的常數通常直接寫下 表示 constant。
那麼上面冗長的式子就能夠用更簡潔的 Notation 表示如下。

因此，往後當我們在描述一個模型時，比起單純的 ，我們更傾向使用如 這種向量與矩陣的表示方式。

判斷好壞

決定好一個模型，接下來要做的就是讓參數調整後與問題十分相像。調整的步驟需要透過評估後再做調整。評估一個模型好壞的函數我們稱為 損失函數(Loss Function) 。

就如同評斷不同種類的事物我們採用的標準會不同，Loss Function 也在不同的情況下會有不同的選擇。現階段請容我暫且不提及其他的 Loss Function，而是到了適切的應用場景再說明。這裡就先只介紹 均方誤差(Mean-Square Error, MSE) 。

均方誤差能夠簡單計算正確資料與預測資料之間的差異。底下是 Notation 的定義。

• 表示資料的總數
• 表示第 筆資料真正的輸出
• 表示第 筆資料模型的輸出
• 表示第 筆資料的輸入

均方誤差的作法如下：

MSE 計算的就是底下橘色線長度的平方總和取平均。

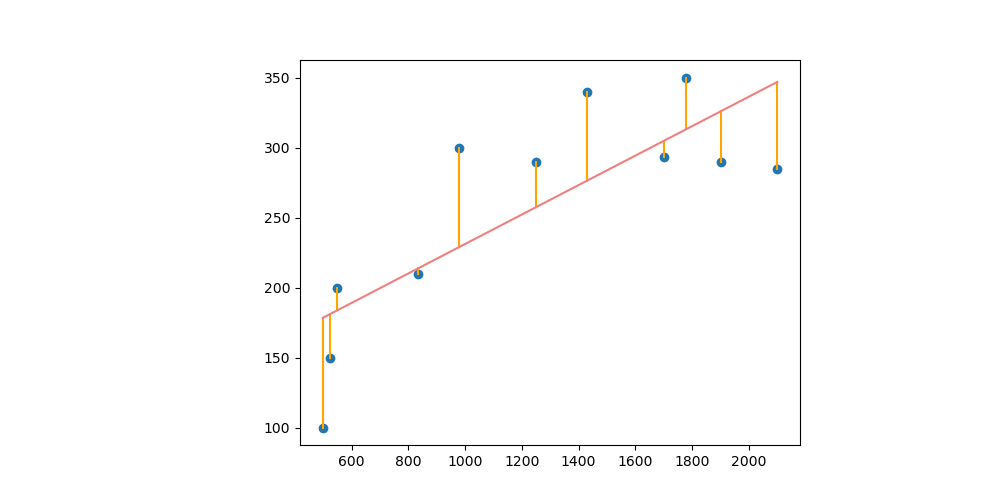
均方誤差僅僅只是計算真實與預測之間的差的平方，然後取平均。當兩個函數相差甚遠時，由於點對之間的距離大，使得誤差也大。反之當兩個函數十分相近，由於點對之間的距離小，誤差也就小了。

預測越好，Loss 越小；預測越糟，Loss 越大

至此我們已經知道如何描述一個模型，又該如何評估模型整體的好壞。不過如同文章最前面提到，想知道的問題是 要如何讓函數擬合問題。評估了整體模型的好壞，還不至於讓我們知道如何更新參數，使得函數得以擬合。

在下一篇將會提到如何依照 Loss Function 給出的結果更新參數。